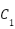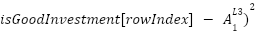
= (
In our last entry, we progressed as far as calculating the cost of a forward propagation through our cost function. In that entry, we concluded that if our cost function is high (not close to 0), we would need to adjust the weights and the biases in our neural network to account for that. This adjustment process is called backpropagation, and this is what we will discuss in this entry.
Just a disclaimer: what follows below involves a significant amount of mathematics. It might seem overwhelming at first, but please give yourself time. The more you review it, the more it will begin to make sense. Also, please ensure you have read the entry on derivatives (see here) before proceeding with this one. It will be quite difficult to follow what is happening here without reading that prerequisite material.
Remember in our section on derivatives, we discussed how you can define the derivative as a slope at a point. Depending on the properties of this slope, you can descend down it until you reach a desired point (i.e., where the cost is zero).
Since we have our cost function (which is MSE), we can find the derivative of this cost function in relation to the variables used to get the final cost, that is, if we know that (from last entry)
= (
= 
= 
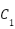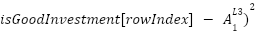
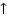
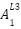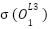
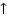
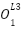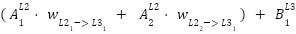
Point 1: Then (from the chain rule)
= 
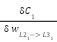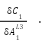
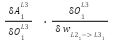
(note: This would be similar for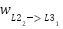 
)
and
= 
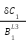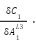
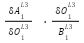
Point 2: From the above we can see that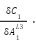 
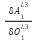are actually consistent. In fact we can call
this the derivative delta and give it the symbols
,
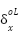where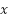 
represent the node (in our case will only ever be 1). Therefore we can say
= 
= 
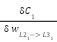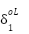
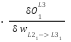
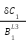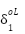
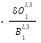
Point 3: Since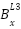 
is a variable to the power of 1 the partial derivative of 
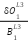is 1. Therefore we can say
= 
= 
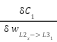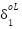
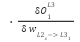
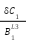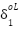
Point 4: With that, we have the derivatives of the weights connected to the output value, and the derivative of the bias connected to the output layer. Since a derivative is, in essence, the slope at a point, we can descend this slope using a learning rate ($\mathcal{L}$) to get new values for the weights and biases. This descent should lead us closer to the minimum of the cost function. Formulaically, this means:
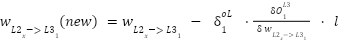
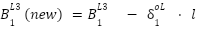
Now that we have our derivative-based formulas for updating our weights and biases, we can substitute the actual derivative into the formula and move on to get the new values.
Point 6: In this
=
)
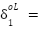
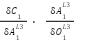
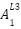Where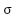 
’ is
the derivative of the activation function used. And since we are using the sigmoid function we get
= 
(
))
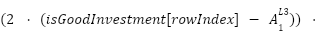
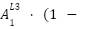
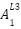Point 7: and (using partial derivatives)
= 
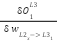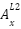
Note: This is the activation value in the second layer (not the last).
Point 3: Therefore for the final layer (with a sigmoid activation function, and MSE cost function) we can say
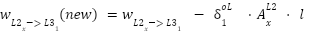
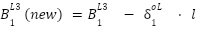
Where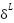 
=
( ))
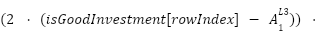
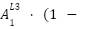
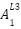Now that we know how to update the weights and biases on the output layer, what about the other layers? The process is essentially the same. The only thing we need to figure out are the derivative deltas of the nodes in that layer. If we can determine the derivative delta for a node, that is,
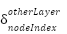
We can repeat the same process to update the bias associated with the node and the weights connecting to it.
But how do we get the derivative delta for a node outside the output layer? Well this is a bit nuanced. The reason being this node is usually a part of other nodes in connecting to a next layer node (for instance 3 nodes in the hidden layer contribute to the output node). Not only that if the next layer nodes were more than 1, the current node influence will be to all the nodes in the next layer.
For this reason our derivative delta for the node is going to be a function of all the associated delta derivatives in the next layer in relation to the activation of the current node and the derivative of the activation at the node. Functionally this is means (using the nodes connected to the output layer)
= 
) 
= ) 
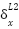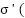
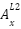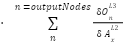
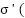
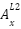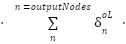
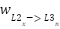
As can be seen from above 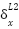is a function of the previous calculated 
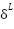, that is, we backpropagate the derivative delta to the next layer, to the
current one.
And that’s it! - Once we have the derivative delta of a node at a particular layer, we repeat the same process to update the weight and bias of that associated node. For instance
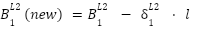
And if we had another hidden layer - we would repeat the same process to obtain the derivative delta for nodes at that layer, backpropagating the current derivative delta, and adjusting the weights and biases.
Lastly as one would expect, once you arrive at the input layer this back propagation stops.